Continents and Oceans:
Topography and Isostasy

River deep, mountain high...

-Tina Turner 


In this lecture period, we wish to learn:

  • Why is there such a difference in the topographic expression of the oceans versus the continents?
  • How do the physical properties of granite and gabbro differ and how does this explain the elevation of the continents and oceans?
  • What structure does the Earth's interior have and how does this material compare to rocks found on the surface of the Earth?
    • Jump to: [The Shape and Size of Earth] [Topography] [Two rocks: Granite and Gabbro] [Isostasy] [Layered Earth] [Summary] [Self-Test]
     
    9/19/2000                                                                                                                                        Format for printing

     

    The Shape and Size of Earth

    A good way to look at a planet is by taking a globe in your hands. The next best thing is a 3D computer rendering. Because 3-dimensional objects are not convenient to carry around, early on in our traveling history the art of map making was invented. Maps of the earth offer 2-dimensional representation of a 3-dimensional object. Because Earth is a sphere, different projections were developed to emphasize different aspects. Perhaps you recall the experience that the shortest distance between points on a map was connected by a curved trajectory. For example, the connections in airline magazines illustrate this property nicely. Another important aspect is the area distortion of many maps. Whereas Alaska is a large state, it appears yet even larger because the E-W distances are commonly the same on maps, but not on a sphere. Such E-W lines are called latitudes, whereas N-S lines are called longitudes. Note that longitudes are all of equal length (circumference of the Earth), but that latitudinal lines are of different length. The longest latitude is the equator, which equals the circumference. 

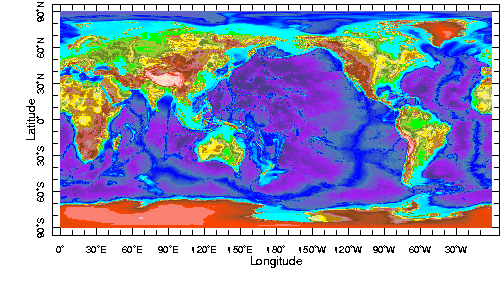
    As soon as civilizations started to travel and trade, knowledge of distances became critical for survival and success. Outside of a few supporters of a flat Earth, the dimensions of our planet were already established long ago. The critical dimensions of the Earth, which approximates a sphere, are defined by its radius, r (= half the diameter). The circumference, C, of a sphere is given by the relationship, C = 2*pi*r ; the area, A, of a sphere is defined by: A = 4*pi*r2, whereas the volume, V, is defined by: 4/3*pi*r3 (pi is ~3.14). 

    Already in the 3rd Century BC, a Greek librarian named Erathosthenes accurately defined the Earth's circumference. The method is very creative. When the sun stands vertical at one point, measured by shining down the bottom of a well, it casts a shadow elsewhere. At a distance of 800 km, Erastosthenes measured an angle of 7.2 degrees from vertical between the top of a wall and the tip of its shadow. Thus an angle of 7.2 degrees describes an arc of 800 km on the Earth's surface. In a full circumference of 360 degrees, this would describe an arc of 360/7.2 x 800 = 40,000 km. Erasthothenes' calculation is within tens of kilometers of today's determination. We can also use trigonometric relationships to determine the radius of the Earth: tan(7.2) = 800km/radius (note that the arc has too be much less than the radius for this particular approximation). Try it.

    Topography

    Even a cursory look at the Earth's globe or a map highlights a fundamental property of the Earth's surface. You see oceans and continents. In fact, more than 70% of the surface is covered by water. 
     
    Figure 1. Earth's Topography.

    At first continents seem merely to be areas that are not covered by water, but the distinction between oceans and continents goes well beyond that. Ultimately the presence of these two physiographic elements sets us apart from neighboring planets, such as similarly-sized Venus. Rather than looking at coastlines only, we will examine the elevation (or topography) of the Earth. Modern satellites are extremely accurate in measuring distances user radar and laser technologies, and a clear picture merges. 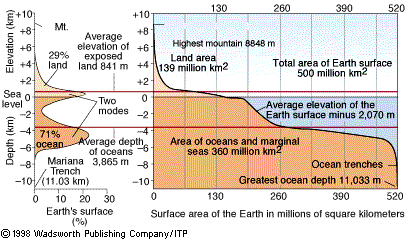Using such observations we create a graph showing the total surface area at a certain elevation, which is called a hypsometric curve. In the figure we show both a hypsometric curve (or cumulative frequency curve) and the more familiar histogram. 
     
     

    First we look at the extremes. The highest point on Earth is Mt. Everest in Nepal, with an elevation of nearly 9 km. The deepest parts of the oceans occur in regions called trenches, which go down to a depth of ~11 km in the Marianas Trench. The total topographic relief on the earth is, therefore, ~20 km. If this sounds like a lot, shrink the Earth (with a diameter of ~12,800 km) down to a fist-sized, polished cueball from a game of pool, and Earth would appear much much smoother. The highest mountain and deepest trench represent only a negligible fraction of the Earth's surface area. Plotting the elevation distribution of the Earth's surface, we see that most of the surface lies below 1 km above sea level and 5 km below sea level. The distribution has two peaks, at ~1 km high ~4 km deep relative to sea level, which characterizes Earth's a bimodal elevation distribution. This means that two elevations dominate the Earth's surface, which roots in the presence of material that makes up the continental areas and material that represents the oceans regions. We'll look at this lateral variation in material (=rock) properties below. Note that Earth's elevation distribution also demonstrates how many of us live just above sea level. Raise sea level by 200m (through melting of continental ice sheets) and see what our continents will look like from today's coastlines (move mouse over image):

    You can further experiment with sea levels and topography, and look at details for your favorite area by going to the LDEO site.

    Two rocks: Granite and Gabbro

    There are hundreds of rock types found at the surface, but blessfully we only need to concern ourselves with about a dozen main types. Rocks are sedimentary, igneous or metamorphic in origin. Sedimentary rocks are deposited at the Earth's surface, whereas igneous and metamorphic rocks are formed deeper in the Earth. Ignoring sedimentary rocks for now, which form only a thin veneer at surface (<10 km thick), we can generalize the composition of the continents and the ocean floor by two igneous rock types: granite and gabbro (or their extrusive equivalents, rhyolite and basalt). Granite is a rock a light-colored consisting mainly of the minerals quartz and feldspar, with various minor phases (such as mica, hornblende). Chemically, granite are high in Si (~70%) and Na, K; it has relatively low Ca and Mg content. Gabbro is a dark-colored rock consisiting mainly of the minerals feldspar, olivine and pyroxene. Chemically, it has low Si, Na and K content, and relatively high Ca and Mg content. These compositions are responsible for a difference in density for these two rock types: granite has a density of ~2800 kg.m-3, whereas gabbro is slightly more dense (~2900 kg.m-3); note that sometimes density is given in g.cm-3 (1000 kg.m-3 = 1 g.cm-3). 
     

    Isostasy

    Flash Media Experiment with Isostasy by changing the block height and density, and the liquid density. Values can be reset by clicking the Reset button. Note that it is not necessary that a solid object floats in a liquid for its application to Earth, where both crust and mantle are solids. 
    From Discover our Earth,  INSTOC/Cornell

    The density difference between granite and gabbro has an important consequence that we can illustrate by simple experiment. If we float a piece of hardwood (like oak) and and a piece of softwood (say, pine) of equal dimensions in a bucket of water, we see that the hardwood rides lower than the pine. The reason is that hardwood has a slightly higher density than softwood, and thus is heavier. Secondly, we float a a piece of wood that is twice as thick as the original piece. The thicker piece sinks deeper and rides higher. Since the weight of a body equals the weight of the liquid is displaces (Archimedes' Principle), thicker or denser blocks will displace more water. 
     

    We apply this experiment to the Earth, with the granite and gabbro as our wood blocks and the deeper mantle as the water. We compare column 1 (atmosphere-granite-mantle) with column 2 (atmosphere-gabbro-mantle); for convenience we combine ocean water and atmosphere. The pressure at the bottom of both columns (at the compensation depth), defined by density x gravity acceleration x height (rho * g * h), must be equal as there is no net material flow along the compensation depth.

     So:

    (rho * g * h)column1 = (rho * g * H)column2; g falls out, so we get: (rho * h)1 = (rho * H)2

    We can now calculate the elevation of the blocks above the compensation depth as a function of its thickness and density. If we know the elevation of a continent, we can determine its thickness. The density difference between granite and gabbro implies that the elevation of gabbro is less than that of continents. Therefore continents are relatively high and ocean floor is relatively low.

    Thickness also is important. We'll first apply these principles to icebergs. Ice floats in sea water because it has a lower density (rhoice=920 kg.m-3, rhoseawater=1025 kg.m-3). Using Newton's Second Law, F = m * g (recall that with m = volume x density) and Archimedes principle, we get: volice . rhoice . g = voldisplaced water . rhowater . g. So, rhoice/rhowater=voldisplaced water/volice. 

    Thus the ratio of displaced water/ice volume equals 0.9 meaning that 90% of an iceberg is below sealevel, whereas only 10% is above sea level. This was already well known at the maiden voyage of the Titanic.

    We can apply this scenario to continental and oceanic crust 'floating' on the mantle. Because both crust and mantle layers are solid, floating is a misleading term.  This calculation is simplified, but gives us a reasonable sense of dimension nonetheless. With a continent/mantle density ratio of 2800/3300=0.85, 10 km thick continent lies ~1.5 km above the reference mantle elevation. For convenience, let's take the mantle reference level ~5 km below sea level. Thus, the average continental elevation of 1 km above sea level represents a continental thickness of ~40 km. The highest mountain ranges, say the Himalayas of Nepal (7-9 km high), therefore require a crustal thickness on the order of 85 km. The average ocean crust is at ~4 km BSL, so its small elevation above mantle reference level indicates that oceanic crust is about 8 km thick.

    Thus, density and thickness contrast between granite and gabbro (continent vs. ocean floor) both promote relatively high continents and relatively low ocean floor. Density, therefore, is a first order property that explains Earth's characteristic bimodal elevation distribution. What about the other planets in our solar system?
     

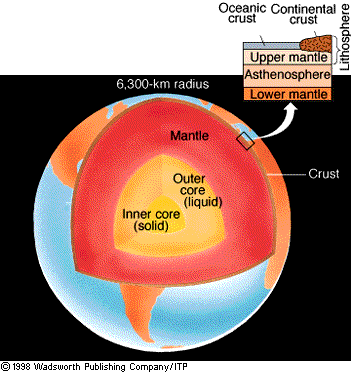
    Layered Earth
     
    How do we know that the whole Earth is not made up of only granite and gabbro, which are the rock types we find near the surface. In other words, how do we know that there is radial variation in Earth?  There are several ways this can be surmised, but one good indicator is average density of Earth. Rocks at the Earth's surface have a density around 3000 kg.m-3, whereas the average density of Earth exceeds 5000 kg.m-3. Let's figure out how we know this and along the way determine a few other properties of our planet.

    Mass and Density of Earth

    Isaac Newton's Second law of motion is: F = m * g
    Newton's Law of Universal gravitation is: F= G * ((m1 * m2) * r--2)
    with F is the gravitational force, m is mass and g is gravity acceleration, which is 9.8 m.sec-2 at the surface. G is the Universal Gravitational Constant, which is 6.67E-11 Nm2.kg-2 based on laboratory measurements. The values m1 and m2 are two masses that attract each other, whereas r is the Earth's radius (6.4E6 m).  For the value of m1, consider a body at the surface of the Earth (say, you) compared to the mass of Earth (m2). 

    Combining these two equations gives:   g = G * (m2 * r--2),which can be solved for m2.
    This results in a mass for Earth of 6E24 kg.

    The volume of the Earth is given by 4/3.p.r3:~1.1E21 m3. Because density equals mass divided by volume, we can calculate Earth's average density of ~5500 kg.m-3. However, density of material deep within Earth is affected by gravitational forces (self-contractions). Without giving the derivation of this effect, the consequence is a density at surface conditions of ~4300 kg.m-3 for average Earth.  These two numbers can be a source of confusion if Earth's average density is given without clarification.

    So, given rock densities of ~3000 kg.m-3, there must be material below that has much greater density than what we find in surface outcrops. In a few places we are able to sample material from depths of a few hundred kilometers, such as inclusion in lavas (called xenoliths), but they still have densities much less than that of the average Earth.  In addition to the models of Earth's early differentiation discussed before, clues come from meteorites that originate from the asteroid belt.  Some meteorites (called, Fe-meteorites) have densities of more than 7000 kg.m-3.  A logical assumption based on the formation of our solar system is that these meteorites reflect properties similar to Earth's core. We can test this inference by looking at the patterns of energy waves as they pass through the Earth. Nature provide us with such a energy source, by the occurrence of earthquakes, which nicely support our layered Earth model.

    Summary

    Two elevations dominate the Earth's surface: that of the continents and that of the oceans. This observation can be explained by the difference in density of the rocks that are characteristic of these areas. More specifically, granite is a common igneous rock that approximates the composition of the continents, which is less dense than gabbro, the dominant rock type of the oceanic crust.

    The Earth's structure is layered and this stratification exists because of differences in density. Rocks at the surface of the Earth have a density that is lower than the average density of the entire Earth. This means that the material below the surface must have a much greater density than rocks that we find at the surface.
     
     

    Take the Self-Test for this lecture.

    Copyright and Use Statement: Regents of the University of Michigan
    Images are in the public domain unless indicated otherwise.